This is me about to do a 100' rope swing off El Capitan in Yosemite
Actually, I guess this was taken just after swinging, but the rest is right
Well, actually, the swing was only 30', but everything else is definitely the truth
Okay, fine, it wasn't El Capitan, it was just a rock in Delaware, but I swear the rest is real
Fine, I didn't actually swing, I just held a rope, but the idea is the same
Alright, alright, I'll come clean: the original story was true
Jamie Simon
I'm a final-year PhD student in the physics department at UC Berkeley, aiming to use tools from theoretical physics to build fundamental understanding of deep neural networks. I'm advised by Mike DeWeese and supported by an NSF Graduate Research Fellowship. I'm also a research fellow at Imbue. In my free time, I like running, puzzles, spending time in forests, and balancing things.
A lot of my papers have come about from helping people doing (mostly) empirical ML research come up with good minimal theoretical toy models that explain effects they're seeing
[1,2,3,4,5].
Some of these ideas came about from quick initial conversations! If you've got a curious empirical phenomenon you're trying to explain, feel free to reach out :)
If you'd like get emailed when I post new blogposts, you can sign up here.
Research
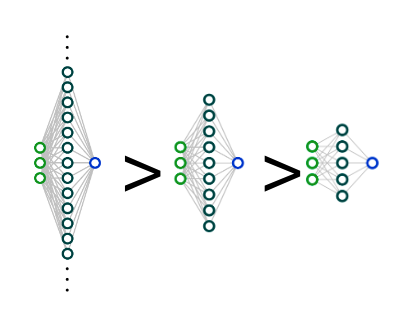
More is better: when infinite overparameterization is optimal and overfitting is obligatory
Explaining mysteries of modern ML with the toy model of RF regressionWe give a theory of the generalization of random feature models. We conclude they perform better with more parameters, more data, and less regularization, putting theoretical backing to these observations in modern ML. This gives a fairly solid mathematical picture to replace classical intuitions about the risks of overparameterization and overfitting. Our picture of the generalization of RF models takes the form of some nice closed-form equations we think can be used to answer lots of other questions.
ICLR '24 [arXiv]
A spectral condition for feature learning
A simple picture of feature learning in wide netsWe give a simple scaling treatment of feature learning in wide networks in terms of the spectral norm of weight matrices. If you want to understand the "mu-parameterization," this is probably the easiest place to start ca. 2024.
On the stepwise nature of self-supervised learning
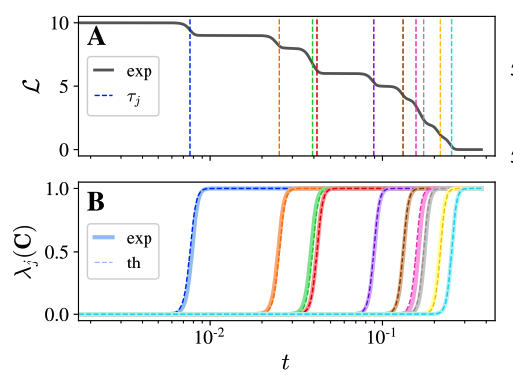
A theory of the training dynamics of contrastive learningWe give a theory of the training dynamics of contrastive self-supervised learning and validate it empirically. We find that representations are learned one dimension at a time in a stepwise fashion -- that is, the rank of the model's final representations increases by one at each step. Our theory is derived for linearized models, but we clearly see our stepwise phenomenon even for ResNets trained on image data. Large-scale ML mostly uses unsupervised and self-supervised training these days, and we describe a behavior we think is fairly generic in SSL.
ICML '23 [arXiv]
You can just put up a poster at ICML and nobody will stop you
Exposing vulnerabilities in the conference review systemA perennial problem in machine learning research has been how to most efficiently have a poster at ICML. In this work, we show that one can bypass OpenReview via a simple “FedEx trick," similar to yet entirely different from the kernel trick in machine learning. (I'm putting this here as an easter egg to see if people actually read these. If you see this and saw + were amused by the original poster, feel free to drop me a line :))
ICML '23 [viral tweet]
Reverse engineering the neural tangent kernel
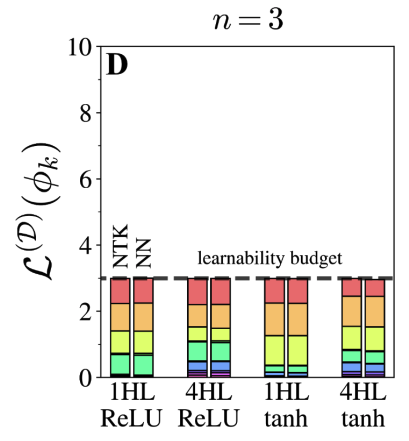
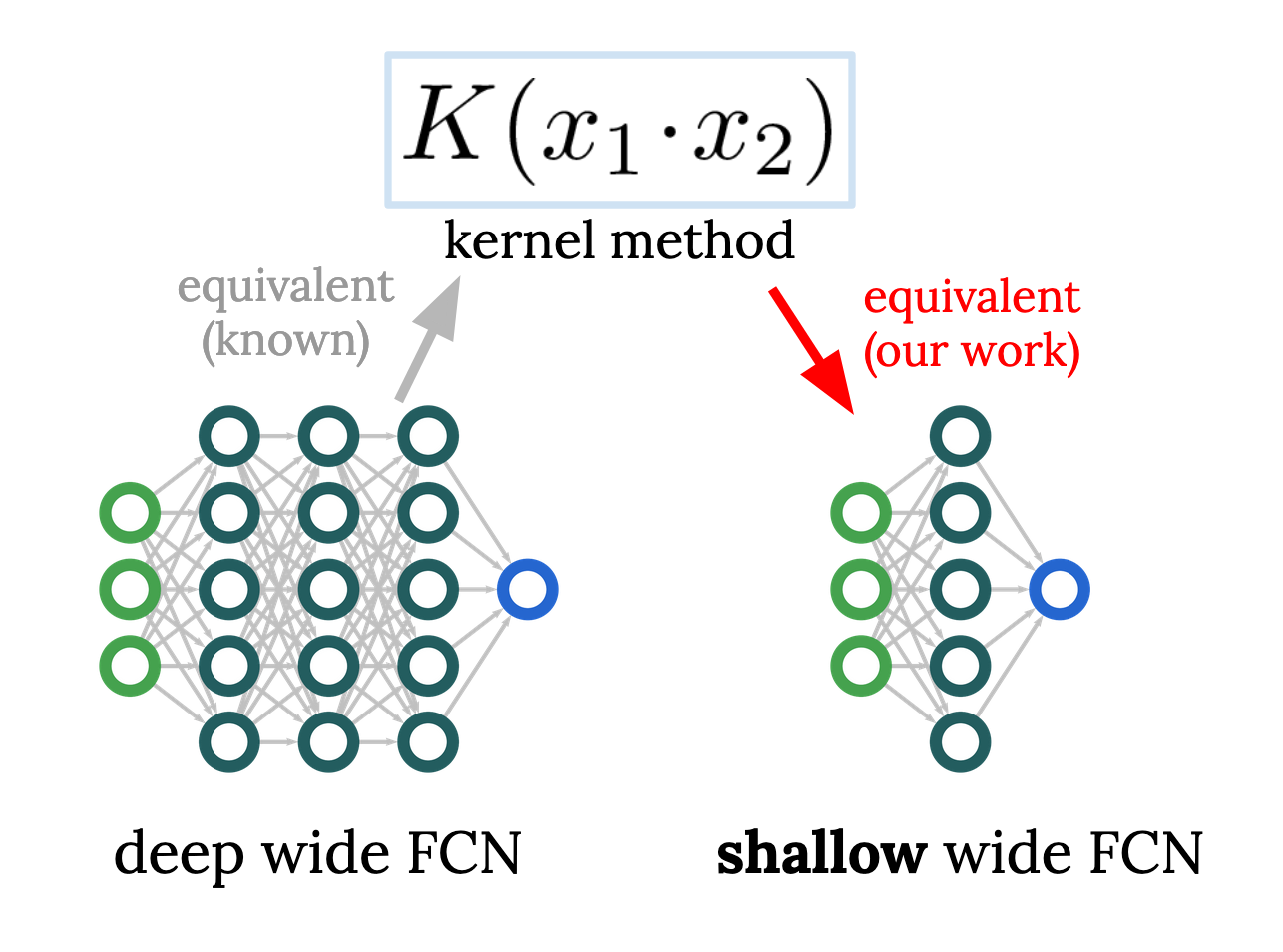
A first-principles method for the design of fully-connected architecturesMuch of our understanding of artificial neural networks stems from the fact that, in the infinite-width limit, they turn out to be equivalent to a class of simple models called kernel regression. Given a wide network architecture, it's well-known how to find the equivalent kernel method, allowing us to study popular models in the infinite-width limit. In work with Sajant Anand, we invert this mapping for fully-connected nets (FCNs), allowing one to start from a desired rotation-invariant kernel and design a network (i.e. choose an activation function) to achieve it. Remarkably, achieving any such kernel requires only one hidden layer, raising questions about conventional wisdom on the benefits of depth. This allows surprising experiments, like designing a 1HL FCN that trains and generalizes like a deep ReLU FCN. This ability to design nets with desired kernels is a step towards deriving good net architectures from first principles, a longtime dream of the field of machine learning.
Benign, tempered or catastrophic: a taxonomy of overfitting
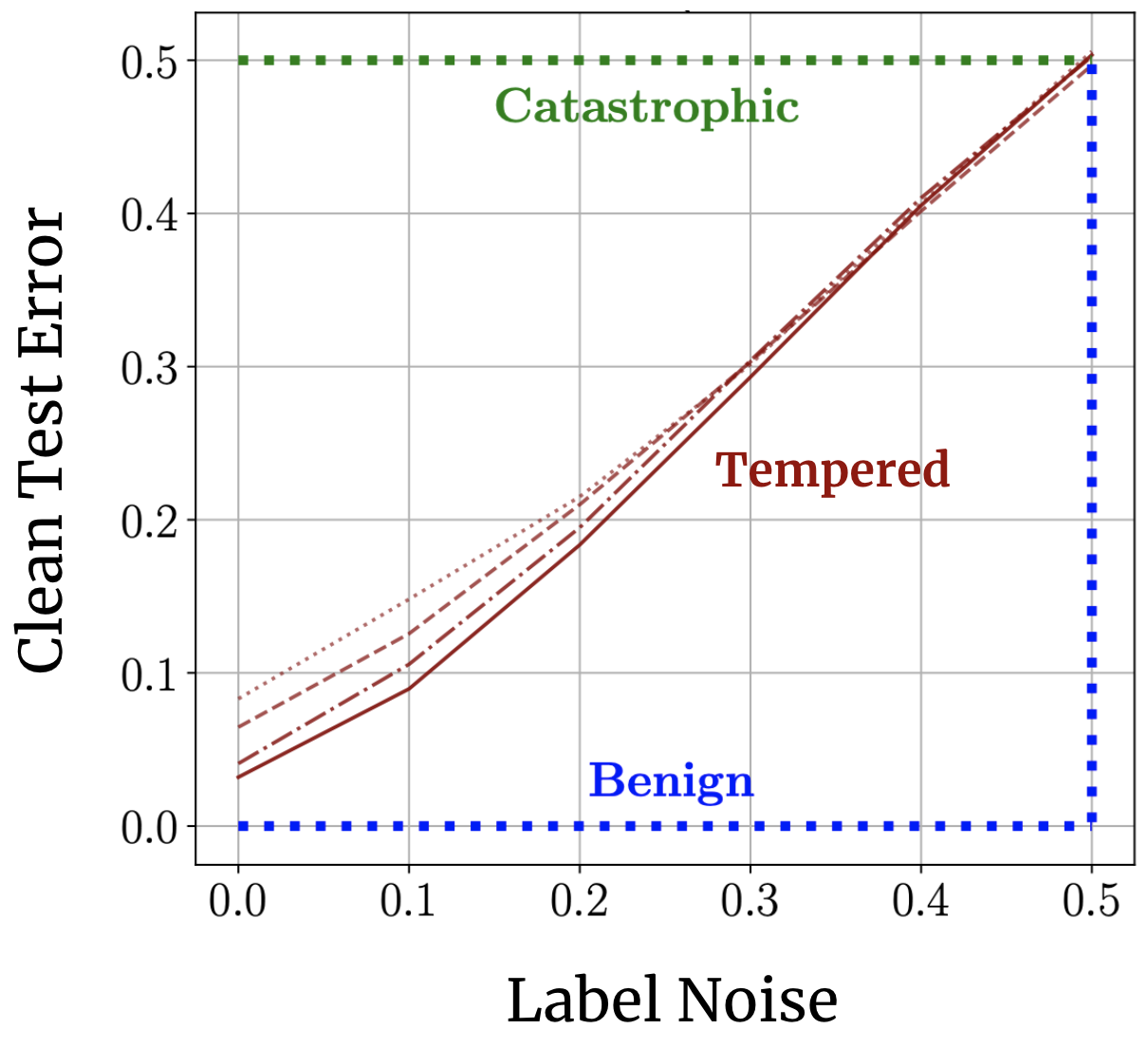
How bad is neural network overfitting?Classical wisdom holds that overparameterization is harmful. Neural nets defy this wisdom, generalizing well despite their overparameterization and interpolation of the training data. How can we understand this discrepancy? Recent landmark papers have explored the concept of benign overfitting -- a phenomenon in which certain models can interpolate noisy data without harming generalization -- suggesting that that neural nets may fit benignly. In this work with Neil Mallinar, Preetum Nakkiran, and others, we put this idea to the empirical test, giving a new characterization of neural network overfitting and noise sensitivity. We find that neural networks trained to interpolation do not overfit benignly, but neither do they exhibit the catastrophic overfitting foretold by classical wisdom: instead, they usually lie in a third, intermediate regime we call tempered overfitting. I found that we can understand these three regimes of overfitting analytically for kernel regression (a toy model for neural networks), and I proved a simple "trichotomy theorem" relating a kernel's eigenspectrum to its overfitting behavior.
NeurIPS '22 [arXiv]
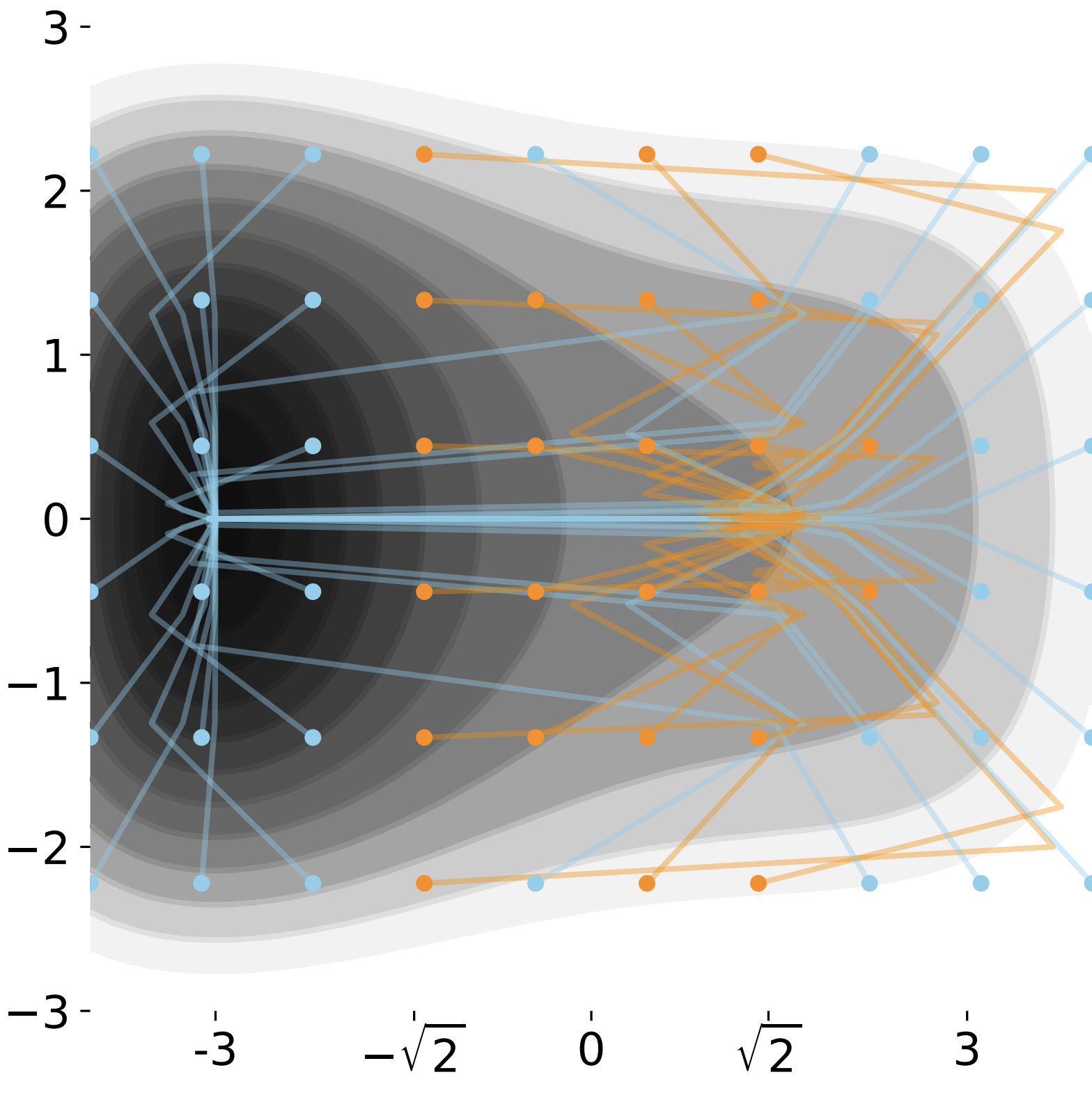
Critical point-finding methods reveal gradient-flat regions of deep network losses
Exposing flaws in widely-used critical-point-finding methodsDespite how common and useful neural networks are, there are still basic mysteries about how they work, many related to properties of their loss surfaces. In this project, led by Charles Frye, we tested Newton methods (common tools for optimization and exploring function structure) on loss surfaces. We found that, as opposed to finding critical points as designed, in practice Newton methods almost always converged to a different, spurious class of points which we described. Giving simple visualizable examples to illustrate the problem, we showed that some major studies using Newton methods on loss surfaces probably misinterpreted their results. Our paper is here.
(2021) [Neural Computation] [arXiv] [code]
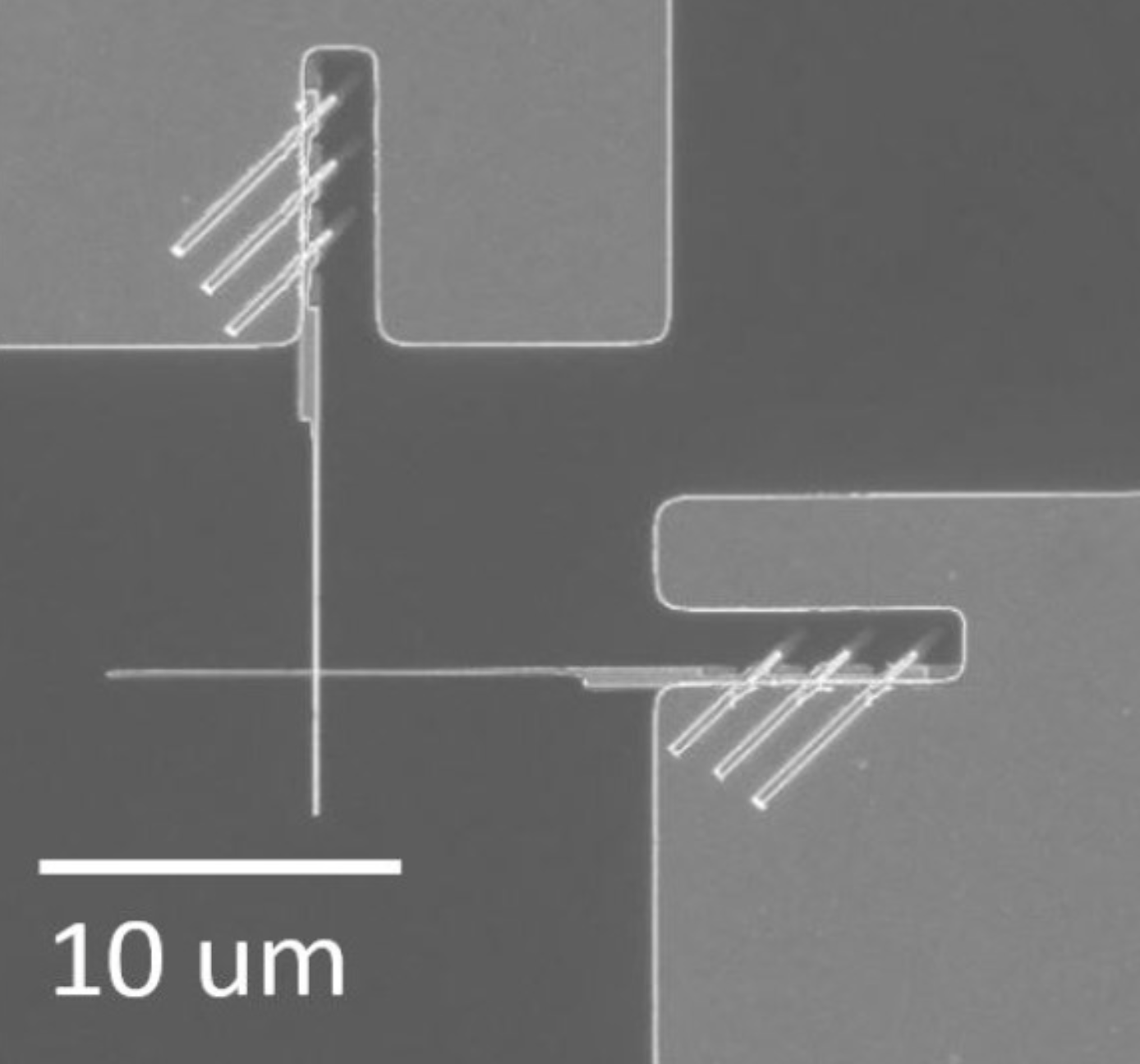
Simplified Josephson-junction fabrication process for reproducibly high-performance superconducting qubits
A faster method to make Josephson junctionsIn the spring and summer of 2019 I worked in the lab of Prof. Per Delsing developing nanofabrication methods for Josephson junctions, ubiquitous components in superconducting circuitry. My main project was a study of how junctions age in the months after fabrication, but my biggest contribution was elsewhere: Anita Fadavi, Amr Osman and I developed a junction design that is faster to fabricate by one lithography step, or potentially several days of work.
(2021) [Applied Physics Letters]
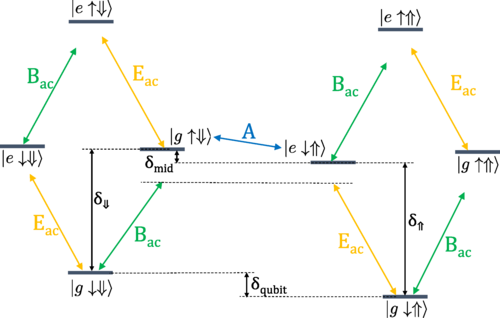
Fast noise-resistant control of donor nuclear spin qubits in silicon
Better control schemes for for spin qubitsQubits decohere and lose their quantum information when uncontrollably coupled to their environment. Nuclear spin qubits in silicon are extremely weakly coupled to their environment, giving them long coherence times (up to minutes), but that same weak coupling makes quickly controlling them difficult. Advised by Prof. Sophia Economou, I came up with schemes for driving nuclear spin qubits that give fast, noise-resistant arbitrary single-qubit gates. The most important gate is a long sweep that effectively turns uncertainty in electric field (charge noise) into uncertainty in time, which can be accounted for by corrective gates. We also show two-qubit gates.
Puzzles
While a senior in undergrad, I started a puzzlehunt called the VT Hunt with Bennett Witcher. It became a university tradition, with the 2019-22 VT Hunts each drawing 1000-2000 participants and raising money for charities, and I've stayed involved as a mentor. I've also helped concoct six other puzzle events starting in high school. A few of my favorite puzzles I've made are below. They're roughly ordered from easiest to hardest, so you can pick where to start.
