Research
Understanding deep learning will be one of the grand scientific challenges of the early 21st century. I want to develop fundamental theory to explain how neural networks learn. This is a big project that in total will require at least some theory of the data, a picture of the dynamics of neural net optimization, and a picture of how the model pulls out patterns from the data during this optimization process. We've seen a lot of progress in the past decade, I'm optimistic.
This page gives a sketch of my major research threads, with each paper annotated to explain how it fits into its larger line of work and/or how I suggest you read it. The best articulation of my research philosophy's currently here. I'm a physicist by training, and I tend to take a first-principles, bottom-up, dynamics-first approach to the task of theorycraft.
A lot of my papers have come about from helping people doing (mostly) empirical ML research come up with good minimal theoretical toy models that explain effects they're seeing [1,2,3,4,5]. Some of these ideas came about from quick initial conversations! If you've got a curious empirical phenomenon you're trying to explain, please reach out.
Developing + using the theory of kernel regression
Kernel ridge regression (KRR) is a primitive learning algorithm that looks a lot like deep learning in some ways (e.g., as a model of overparameterized optimization). It's strictly simpler, and any question you can't answer for KRR, you can't answer for deep learning, so you should ask your questions about KRR first to get your thinking straight. I've done a lot of that. KRR is the only learning algorithm for which we have a simple, general, and verifiable theory of generalization. I've helped build this hammer and hit a lot of nails with it.
Dhruva Karkada*, Joey Turnbull*, Yuxi Liu, James B. Simon
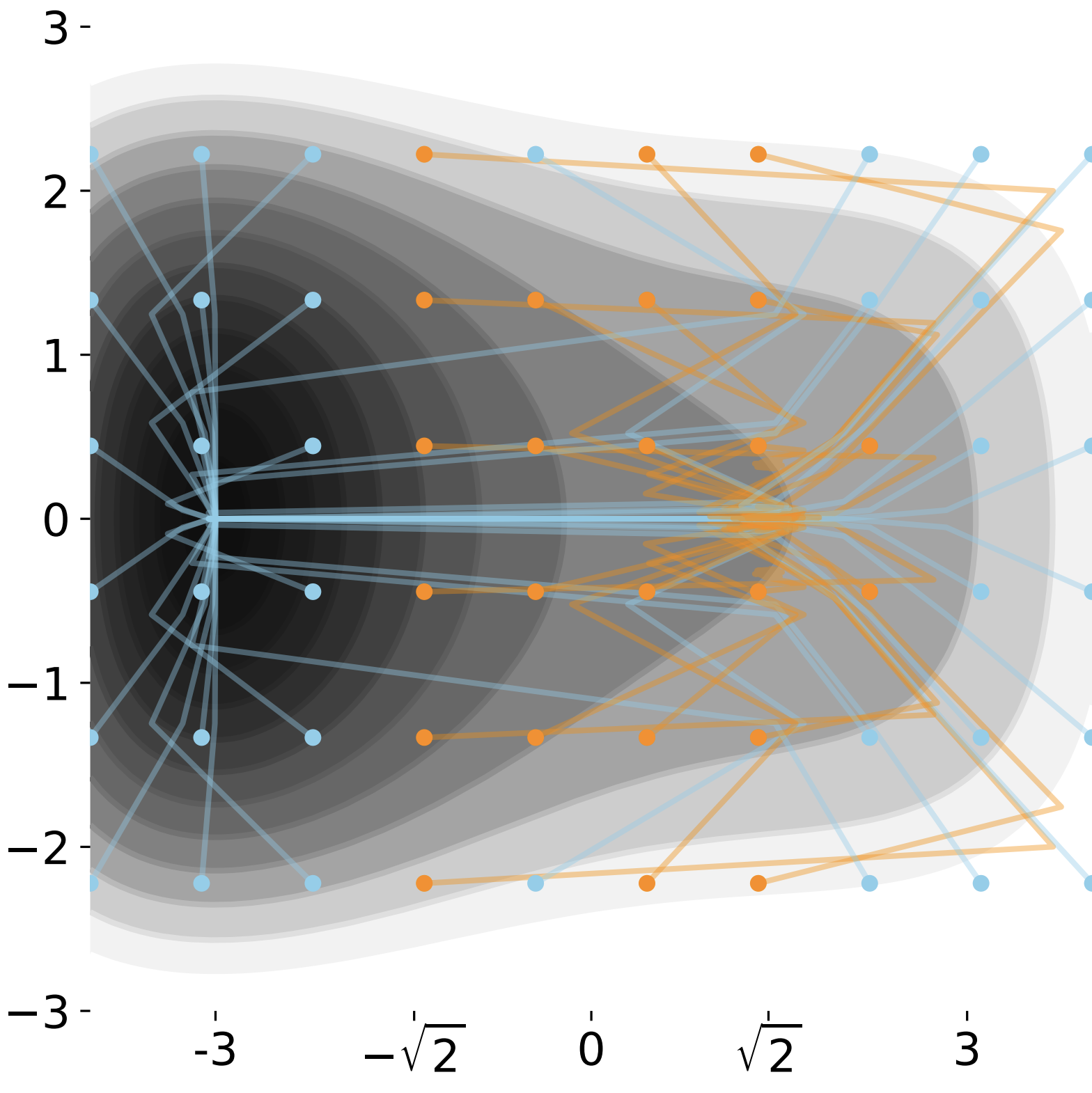
We study KRR with rotation-invariant kernels. We give a theoretical framework that predicts learning curves (test risk vs. sample size) from only two measurements: the empirical data covariance matrix and an empirical polynomial decomposition of the target function $f_*$.
This is possible because it turns out the kernel's eigenfunctions are approximately Hermite polynomials (and approximately insensitive to the actual choice of rotation-invariant kernel). We capture this idea mathematically as the Hermite eigenstructure ansatz, prove it in informative limiting cases for Gaussian data, and validate it empirically for several real image datasets.
We did this project as a stepping stone towards a theory of MLPs. We needed a rudimentary theory of the structure of the data, and now we have one. As we show in the paper, even feature-learning MLPs seem to learn Hermite monomials in an order predicted by the HEA! This paper worked far better than any of us expected, which when doing science, is a good sign you're on to something.
This was my first paper functioning as a PI. It's also my best work -- my coauthors did a remarkable job.
James B. Simon, Dhruva Karkada, Nikhil Ghosh, Mikhail Belkin
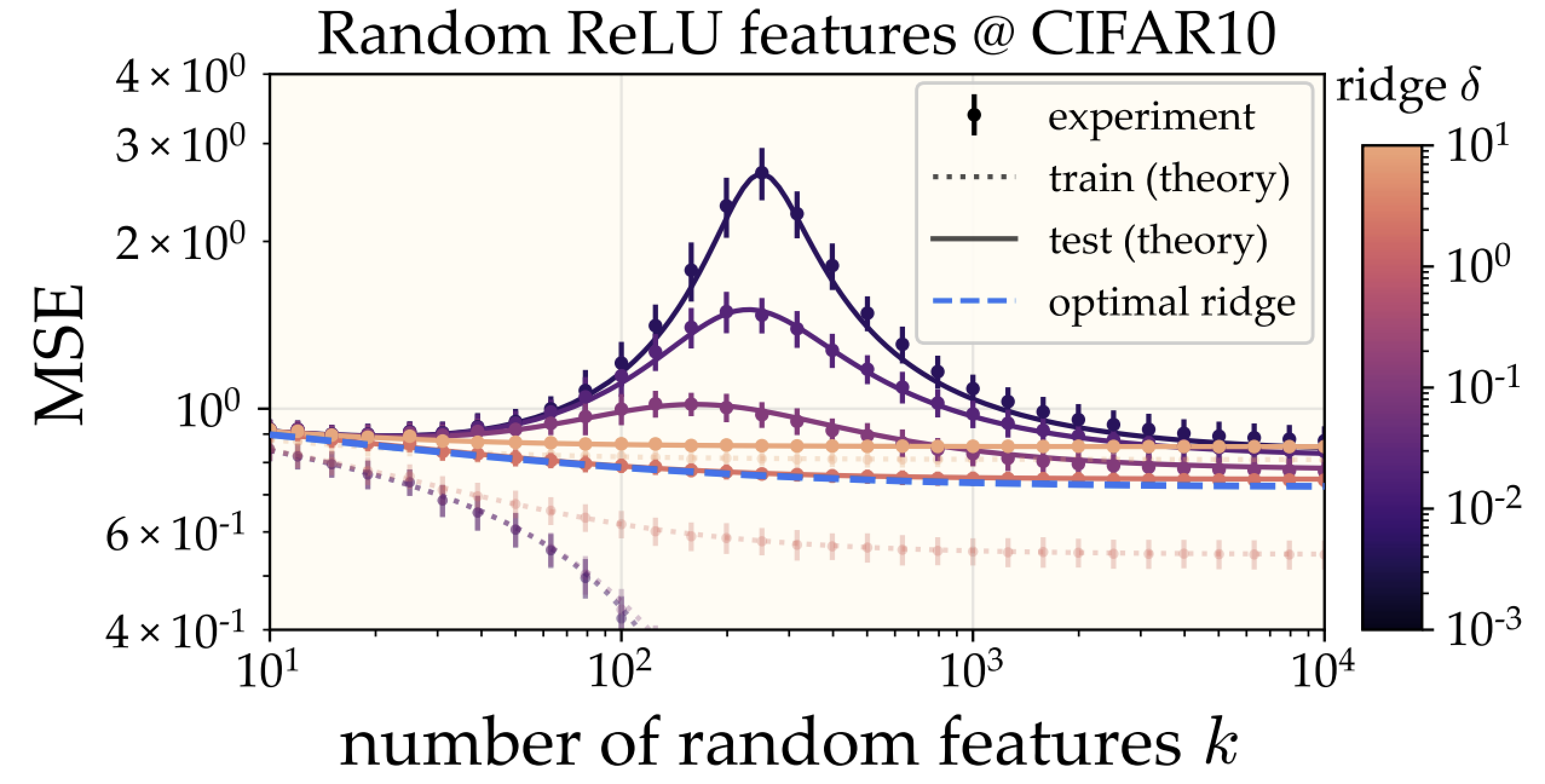
Our main contribution here a theory of the generalization of random feature models. It's a simple eigenframework which generalizes the one for KRR. With it, we conclude that random feature regression performs better with more parameters, more data, and less regularization, putting theoretical backing to these observations in modern ML. This gives a fairly solid mathematical picture to replace classical intuitions about the risks of overparameterization and overfitting. The eigenframework here can probably be used to answer a lot of other questions.
Lijia Zhou, James B. Simon, Gal Vardi, Nathan Srebro
In this paper, we work backwards from the KRR eigenframework, which is
omniscient in the sense that it assumes knowledge of the target function, to an
agnostic theory which does not. It's similar in goal to
this blogpost.
Neil Mallinar*, James B. Simon*, Amirhesam Abedsoltan, Parthe Pandit, Misha Belkin, Preetum Nakkiran
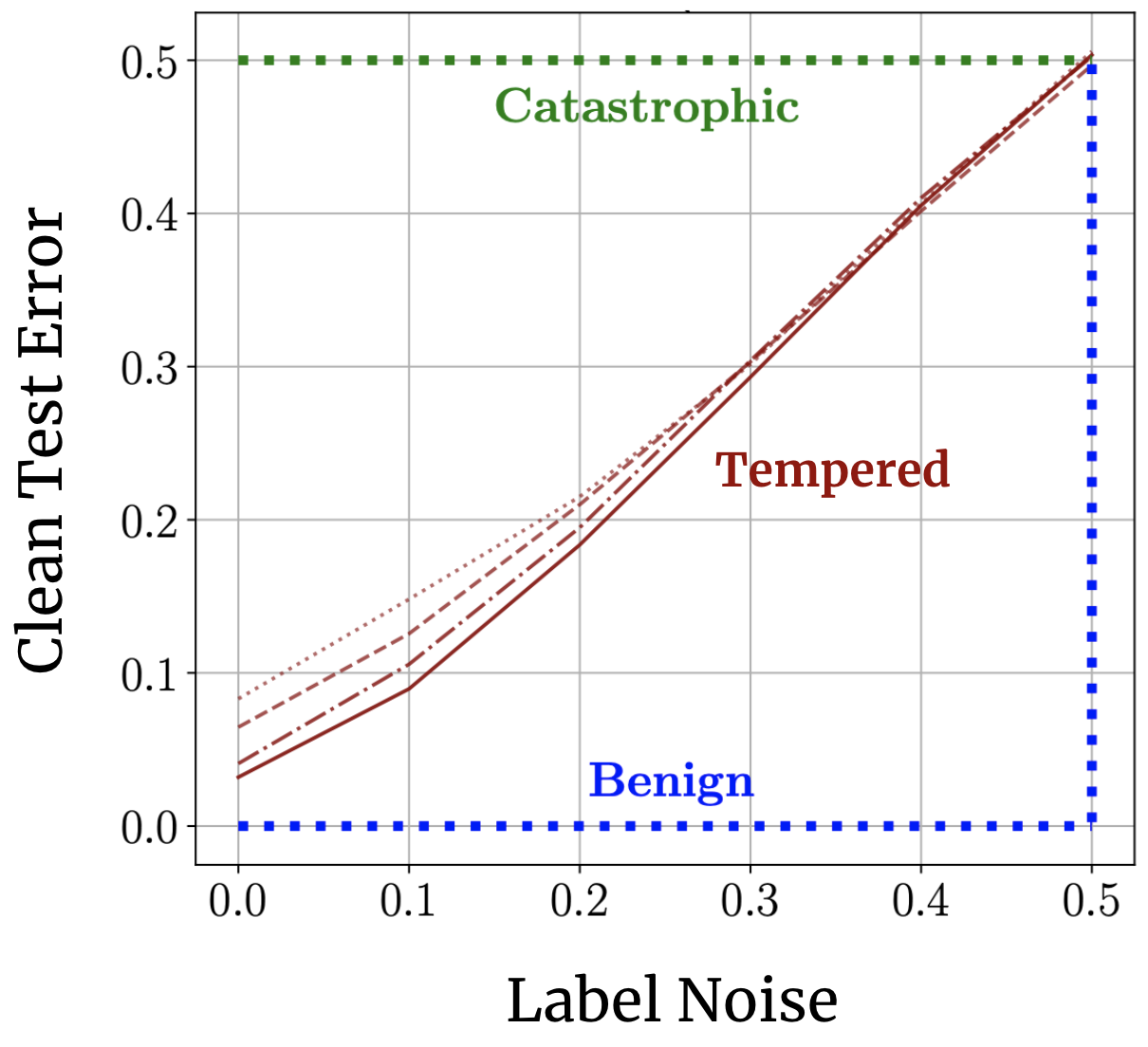
Classical wisdom holds that overparameterization is harmful. Neural nets defy this wisdom, generalizing well despite their overparameterization and interpolation of the training data. What gives? How can we understand this discrepancy?
Recent landmark papers have explored the concept of benign overfitting -- a phenomenon in which certain models can interpolate noisy data without harming generalization -- suggesting that that neural nets may fit benignly. Here we put this idea to the empirical test, giving a new characterization of neural network overfitting and noise sensitivity. We find that neural networks trained to interpolation do not overfit benignly, but neither do they exhibit the catastrophic overfitting foretold by classical wisdom: instead, they usually lie in a third, intermediate regime we call tempered overfitting. I found that we can understand these three regimes of overfitting analytically for kernel regression (a toy model for neural networks), and I proved a simple "trichotomy theorem" relating a kernel's eigenspectrum to its overfitting behavior.
James B. Simon
A short note connecting optimal kernel adaptation to the data to a Bayesian view of target functions. This hasn't been useful since, but maybe someday.
James B. Simon, Madeline Dickens, Dhruva Karkada, Michael R. DeWeese
This is the paper that started this whole sequence for me. Maddie and I managed to derive a simple, physicsy eigenframework for the generalization of KRR. It turned out others had beat us to it, but I was captivated by the beauty of the equations, so we published this paper giving what I think is still the simplest and most accessible version of the theory, plus a handful of applications, plus a surprising connection to quantum physics. If you're not familiar with these ideas and want to study generalization in machine learning, I strongly recommend you read this paper or one of the related ones we cite.
Stepwise learning dynamics
In certain regimes, neural nets show staircase-like loss curves over the course of optimization, with plateaus punctuated by sudden drops. This sort of dynamics is called "stepwise," "saddle-to-saddle," or "incremental" learning, and it has the flavor of greedy low-rank optimization. The dynamics in these cases is often easier to understand than in more traditional regimes, so it's worth understanding what's going on to look for generalizing insights.
Dhruva Karkada, James B. Simon, Yasaman Bahri, Michael R. DeWeese
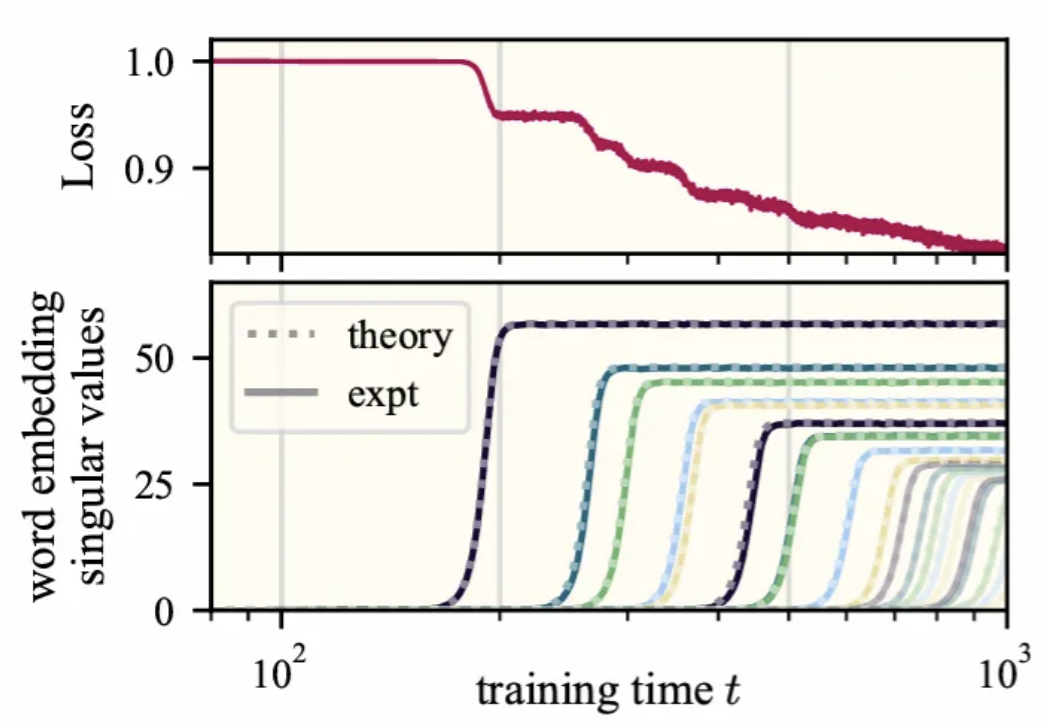
We show that word2vec exhibits stepwise learning, and even better, the early steps correspond to interpretable semantic concepts in the vocabulary. This is a promising bridge for connecting fundamental theory to mechanistic interpretability.
Daniel Kunin, Giovanni Luca Marchetti, Feng Chen, Dhruva Karkada, James B. Simon, Michael R. DeWeese, Surya Ganguli, Nina Miolane
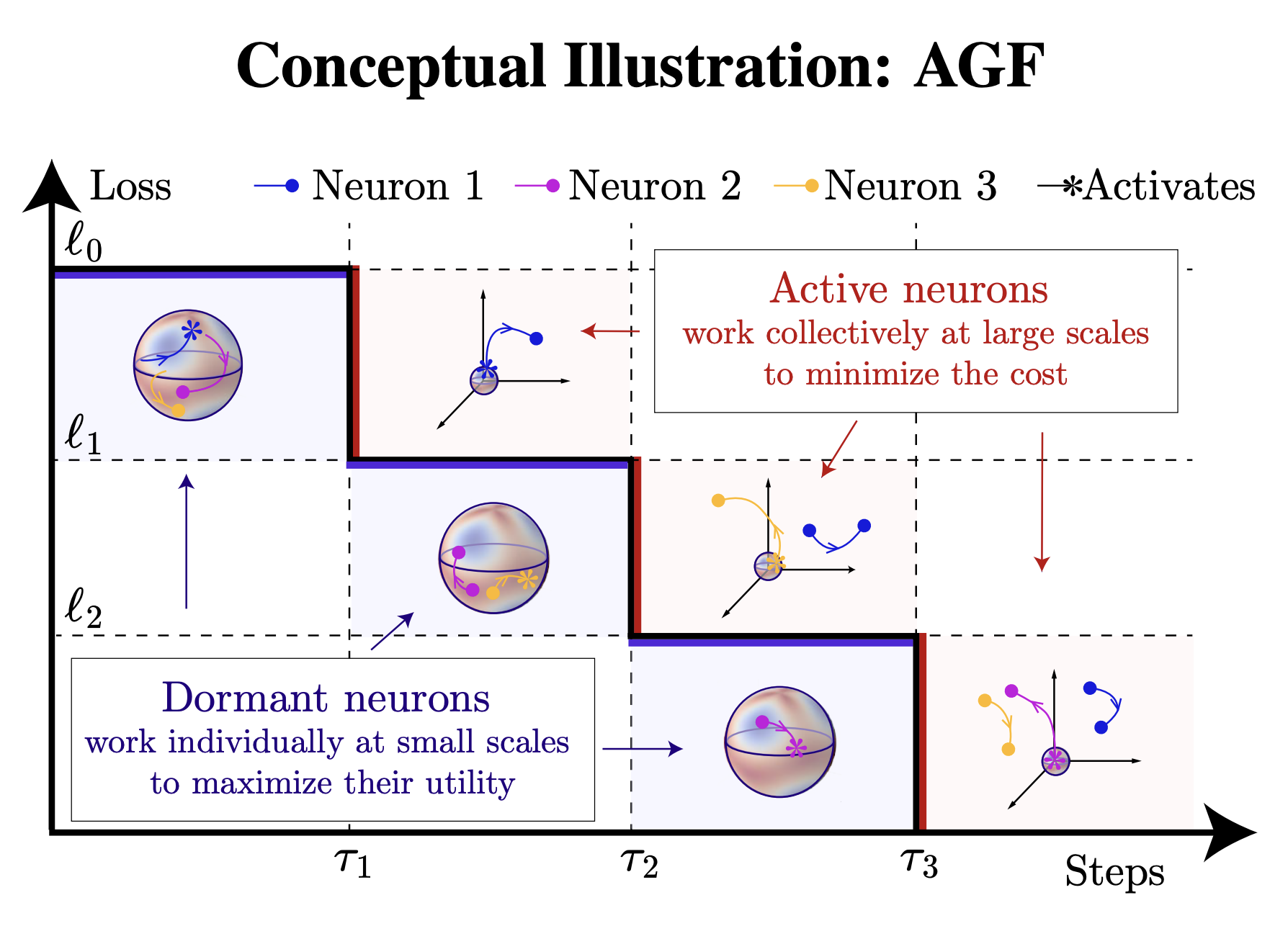
We give an explicit algorithmic description of feature learning in some shallow neural networks trained from small init. In this picture, the model alternates between alignment phases, in which dormant neurons align with the current residual gradient, and growth phases, in which a newly grown neuron joints the community, which collectively settles into a new locally optimal configuration.
Ioannis Bantzis, James B. Simon, Arthur Jacot
Do general deep neural networks show stepwise learning dynamics from small initialization? Empirically, it's surprisingly hard to tell. Theoretically, it's also surprisingly hard to tell. In this paper, we take the first step by studying the first step a deep $\textrm{ReLU}$ net provably has at least one plateau-and-drop step, and we characterize this first step, showing that the growth direction is rank-one in almost all weight matrices.
James B. Simon, Maksis Knutins, Liu Ziyin, Daniel Geisz, Abraham J. Fetterman, Joshua Albrecht
This is the paper that started this sequence for me. We noticed that self-supervised models sometimes exhibited stepwise loss curves, and I developed a kernel theory that explains why. The theory is exact in the neural tangent kernel regime. The theory and supporting empirics suggest that we can understand self-supervised models as building their representations a few directions at a time, working in a low-rank subspace at any given moment.
Scaling dynamics and hyperparameters of feature learning
A central tenet of the developing science of deep learning is that you should study your hyperparameters, because if you don't control for them, they'll confound whatever conclusion you're attempting to draw. In these papers, we study hyperparameters related to feature learning. These scaling relationships help lay down foundations for future science.
Alexander Atanasov*, Alexandru Meterez*, James B. Simon*, Cengiz Pehlevan
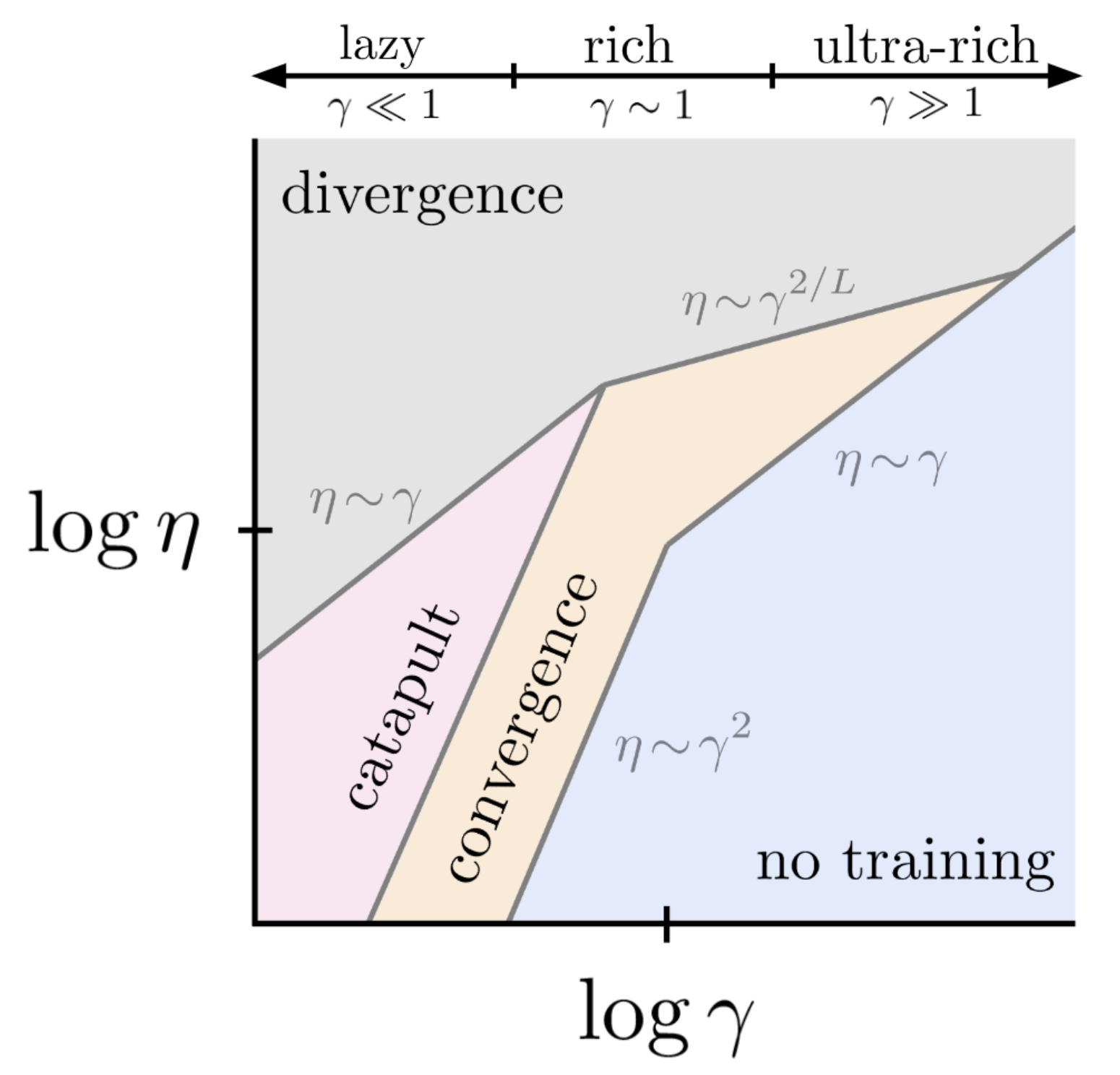
We disentangle the network richness parameter $\gamma$ from the learning rate $\eta$, identifying scaling relationships and giving a phase diagram. We give a definition and characterization of the ultra-rich regime, which lives $\gamma \gg 1$ beyond the rich regime. Training in the ultra-rich regime often shows stepwise learning and is conceptually related to training from small initialization. It seems to be mathematically simpler than the rich regime but no less performant (at least given long enough to train), and we came away from this thinking it is a useful subject for future theoretical research.
Greg Yang*, James B. Simon*, Jeremy Bernstein*
We give a simple scaling treatment of feature learning in wide networks in terms of the spectral norm of weight matrices. If you want to understand the $\mu$-parameterization, this is probably the easiest place to start.
My thesis
James Simon
The introduction here is probably a good resource for new students in DL theory to read to get some bearings. The rest is my papers stapled together with some personal history thrown in.
Other machine learning theory
Odds and ends.
Enric Boix-Adserà*, Neil Mallinar*, James B. Simon, Mikhail Belkin
I quite like the neural feature ansatz, but it's not derivable from first principles, and I was (and remain) convinced it's not quite the right object to study. This paper gives an alternative which does provably come from a first-principles calculation and serves basically the same purposes.
Jimmy Neuron, Chet G. P. Tee, Ada Grahd
Did you know you can just do things?
James B. Simon, Sajant Anand, Michael R. DeWeese
This was a cute idea with some surprisingly nice math. It's where I first used Hermite polynomials, which would later return. It was a pretty idea, but I no longer believe in it.
Liu Ziyin, Botao Li, James B. Simon, Masahito Ueda
A cute observation about pathological cases of SGD loss landscapes.
Charles G. Frye, James Simon, Neha S. Wadia, Andrew Ligeralde, Michael R. DeWeese, Kristofer E. Bouchard
This was my first ML theory paper!
My past life as a physicist
My academic roots are in physics, and that still informs how I see the world and the development of human knowledge.
Jasper R. Stroud, James B. Simon, Gerd A. Wagner, David F. Plusquellic
Experimental optics work done during summer internship at NIST in 2017.
Amr Osman, James Simon, Andreas Bengtsson, Sandoko Kosen, Philip Krantz, Daniel Perez, Marco Scigliuzzo, Per Delsing, Jonas Bylander, Anita Fadavi Roudsari
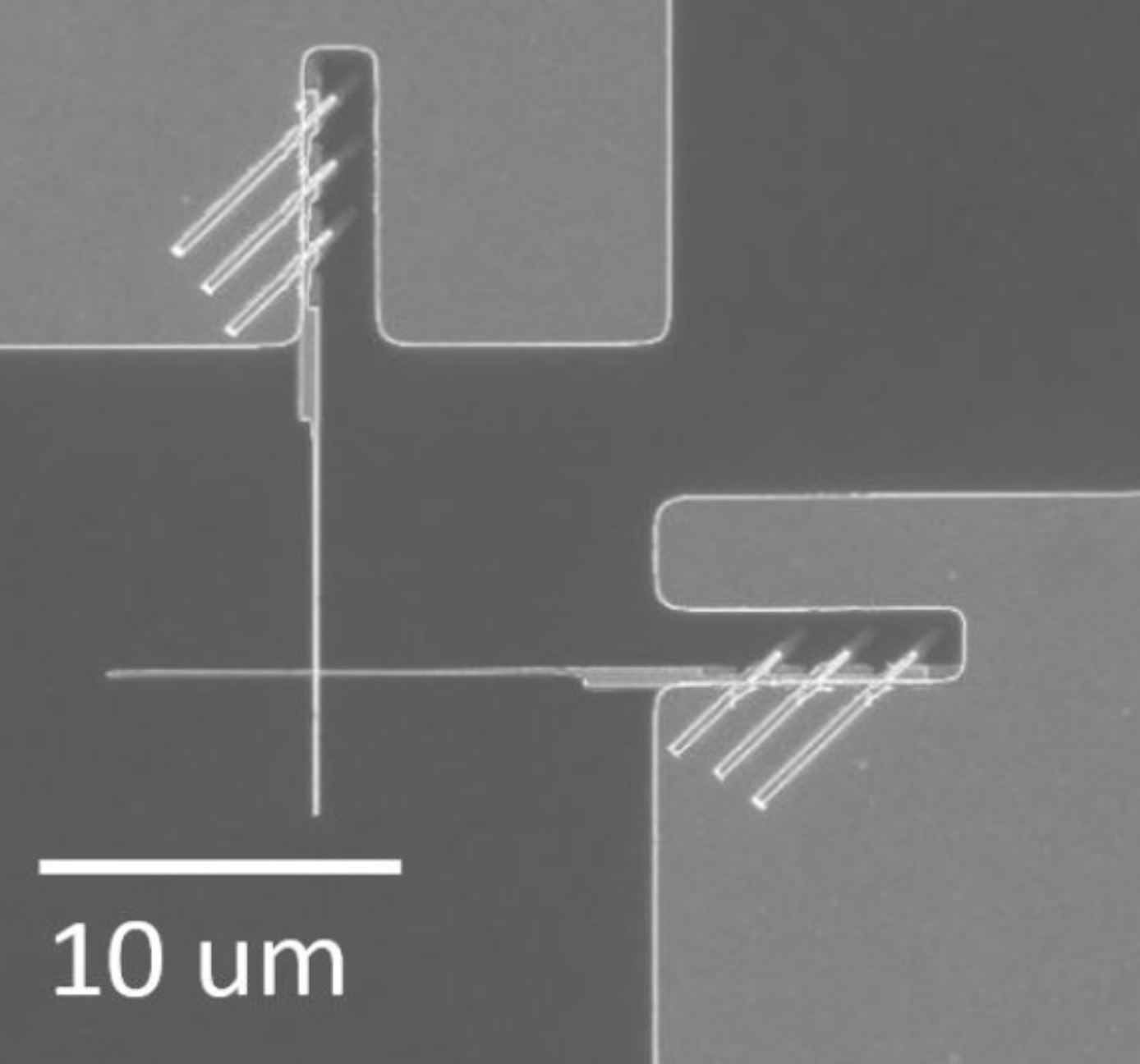
In the spring and summer of 2019 I worked in the lab of Prof. Per Delsing developing nanofabrication methods for Josephson junctions, ubiquitous components in superconducting circuitry. My main project was a study of how junctions age in the months after fabrication, but my biggest contribution was elsewhere: Anita Fadavi, Amr Osman and I developed a junction design that's faster to fabricate by one lithography step, or potentially several days of work.
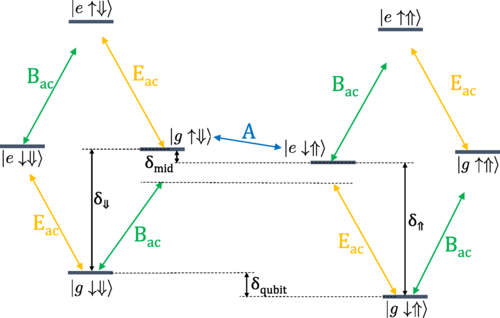
James Simon, F. A. Calderon-Vargas, Edwin Barnes, Sophia E. Economou