A theory of generalization for wide neural nets
This post also appeared on the BAIR blog.
Fig 1. Measures of generalization performance for neural networks trained on four different boolean functions (colors) with varying training set size. For both MSE (left) and learnability (right), theoretical predictions (curves) closely match true performance (dots).
Deep learning has proven a stunning success for countless problems of interest, but this success belies the fact that, at a fundamental level, we do not understand why it works so well. Many empirical phenomena, well-known to deep learning practitioners, remain mysteries to theoreticians. Perhaps the greatest of these mysteries has been the question of generalization: why do the functions learned by neural networks generalize so well to unseen data? From the perspective of classical ML, neural nets’ high performance is a surprise given that they are so overparameterized that they could easily represent countless poorly-generalizing functions.
Questions beginning in “why” are difficult to get a grip on, so we instead take up the following quantitative problem: given a network architecture, a target function \(f\), and a training set of \(n\) random examples, can we efficiently predict the generalization performance of the network’s learned function \(\hat{f}\)? A theory doing this would not only explain why neural networks generalize well on certain functions but would also tell us which function classes a given architecture is well-suited for and potentially even let us choose the best architecture for a given problem from first principles, as well as serving as a general framework for addressing a slew of other deep learning mysteries.
It turns out this is possible: in our recent paper, we derive a first-principles theory that allows one to make accurate predictions of neural network generalization (at least in certain settings). To do so, we make a chain of approximations, first approximating a real network as an idealized infinite-width network, which is known to be equivalent to kernel regression, then deriving new approximate results for the generalization of kernel regression to yield a few simple equations that, despite these approximations, closely predict the generalization performance of the original network.
Finite network \(\approx\) infinite-width network \(=\) kernel regression
A major vein of deep learning theory in the last few years has studied neural networks of infinite width. One might guess that adding more parameters to a network would only make it harder to understand, but, by results akin to central limit theorems for neural nets, infinite-width nets actually take very simple analytical forms. In particular, a wide network trained by gradient descent to zero MSE loss will always learn the function
\[\hat{f}(x) = K(x, \mathcal{D}) K(\mathcal{D}, \mathcal{D})^{-1} f(\mathcal{D}),\]where \(\mathcal{D}\) is the dataset, \(f\) and \(\hat{f}\) are the target and learned functions respectively, and \(K\) is the network’s “neural tangent kernel” (NTK). This is a matrix equation: \(K(x, \mathcal{D})\) is a row vector, \(K(\mathcal{D}, \mathcal{D})\) is the “kernel matrix,” and \(f(\mathcal{D})\) is a column vector. The NTK is different for every architecture class but (at least for wide nets) the same every time you initialize. Because of this equation’s similarity to the normal equation of linear regression, it goes by the name of “kernel regression.”
The sheer simplicity of this equation might make one suspect that an infinite-width net is an absurd idealization with little resemblance to useful networks, but experiments show that, as with the regular central limit theorem, infinite-width results usually kick in sooner than you’d expect, at widths in only the hundreds. Trusting that this first approximation will bear weight, our challenge now is to understand kernel regression.
Approximating the generalization of kernel regression
In deriving the generalization of kernel regression, we get a lot of mileage from a simple trick: we look at the learning problem in the eigenbasis of the kernel. Viewed as a linear operator, the kernel has eigenvalue/vector pairs $(\lambda_i, \phi_i)$ defined by the condition that
\[\int\limits_{\text{input space}} \! \! \! \! K(x, x’) \phi_i(x’) d x’ = \lambda_i \phi_i(x).\]Intuitively speaking, a kernel is a similarity function, and we can interpet its high-eigenvalue eigenfunctions as mapping “similar” points to similar values.
The centerpiece of our analysis is a measure of generalization we call “learnability” which quantifies the alignment of \(f\) and \(\hat{f}\). With a few minor approximations, we derive the extremely simple result that the learnability of each eigenfunction is given by
\[\mathcal{L}(\phi_i) = \frac{\lambda_i}{\lambda_i + C},\]where \(C\) is a constant. Higher learnability is better, and thus this formula tells us that higher-eigenvalue eigenfunctions are easier to learn! Moreover, we show that, as examples are added to the training set, \(C\) gradually decreases from \(\infty\) to \(0\), which means that each mode’s \(\mathcal{L}(\phi_i)\) gradually increases from \(0\) to \(1\), with higher eigenmodes learned first. Models of this form have a strong inductive bias towards learning higher eigenmodes.
We ultimately derive expressions for not just learnability but for all first- and second-order statistics of the learned function, including recovering previous expressions for MSE. We find that these expressions are quite accurate for not just kernel regression but finite networks, too, as illustrated in Fig 1.
No free lunch for neural networks
In addition to approximations for generalization performance, we also prove a simple exact result we call the “no-free-lunch theorem for kernel regression.” The classical no-free-lunch theorem for learning algorithms roughly states that, averaged over all possible target functions \(f\), any supervised learning algorithm has the same expected generalization performance. This makes intuitive sense - after all, most functions look like white noise, with no discernable patterns - but it is also not very useful since the set of “all functions” is usually enormous. Our extension, specific to kernel regression, essentially states that
\[\sum_i \mathcal{L}(\phi_i) = \text{[training set size]}.\]That is, the sum of learnabilities across all kernel eigenfunctions equals the training set size. This exact result paints a vivid picture of a kernel’s inductive bias: the kernel has exactly $\text{[training set size]}$ units of learnability to parcel out to its eigenmodes - no more, no less - and thus eigenmodes are locked in a zero-sum competition to be learned. As shown in Fig 2, we find that this basic conservation law holds exactly for NTK regression and even approximately for finite networks. To our knowledge, this is the first result quantifying such a tradeoff in kernel regression or deep learning. It also applies to linear regression, a special case of kernel regression.
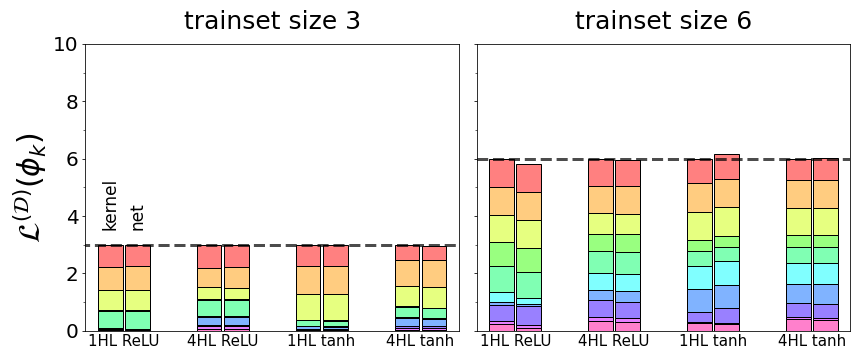
Fig 2. For four different network architectures (fully-connected ReLU and tanh nets with one or four hidden layers), total learnability summed across all eigenfunctions is equal to the size of the training set. Colored components show learnabilities of individual eigenfunctions. For kernel regression with the network’s NTK (left bar in each pair), the sum is exactly the trainset size, while real trained networks (right bar in each pair) sum to approximately the trainset size.
Conclusion
These results show that, despite neural nets’ notorious inscrutability, we can nonetheless hope to understand when and why they work well. As in other fields of science, if we take a step back, we can find simple rules governing what naively appear to be systems of incomprehensible complexity. More work certainly remains to be done before we truly understand deep learning - our theory only applies to MSE loss, and the NTK’s eigensystem is yet unknown in all but the simplest cases - but our results so far suggest we have the makings of a bona fide theory of neural network generalization on our hands.
This post is based on the paper “Neural Tangent Kernel Eigenvalues Accurately Predict Generalization,” which is joint work with labmate Maddie Dickens and advisor Mike DeWeese. We provide code to reproduce all our results. We’d be delighted to field your questions or comments.